TS EAMCET 2018 :: Mathematics :: General questions

• Mathematics - General questions

From a certain population, the probability of choosing a colour blind man is $\frac{1}{20}$ and that of a colour blind woman is  $\frac{1}{10}$ . If a randomly chosen person is found to be colour blind, then the probability that a person is a man is 

Answer:

Explanation:

$P_{CBM}= \frac{1}{20}, P_{CBW}= \frac{1}{10}$

 Person is man= $\frac{1}{2}$ person is woman =$\frac{1}{2}$

$\frac{P_{CBM}}{M}=\frac{\frac{1}{2}.\frac{1}{20}}{\frac{1}{2}.\frac{1}{20}+\frac{1}{2}.\frac{1}{10}}\Rightarrow\frac{.\frac{1}{20}}{\frac{1}{20}+\frac{1}{10}}=\frac{\frac{1}{20}}{\frac{1+2}{20}}\Rightarrow\frac{1}{3}$

 Two distributions A and B have the same mean. If their  coefficients of variation are 6 and 2 respectively  and $\sigma _{A}, \sigma_{B}$ are their standard deviations, then

Answer:

Explanation:

Let   $\overline{x}_{A}=\overline{x}_{B}=x$

$\frac{\sigma_{A}}{\overline{x}_{A}}\times100=6,\frac{\sigma_{B}}{\overline{x}_{B}}\times100=2$

$\frac{\sigma_{A}}{x}\times100=6,\frac{\sigma_{B}}{x}\times100=2$

$\frac{\sigma_{A}\times100}{6}=x,\frac{\sigma_{B}\times100}{2}=x$

$\Rightarrow$     $\frac{\sigma_{A}\times100}{6}=\frac{\sigma_{B}\times100}{2}\Rightarrow \sigma_{A}=3\sigma_{B}$

The equation of the  plane passing through the points with position vectors $A(2\hat{i}+6\hat{j}-6\hat{k})$, $B(-3\hat{i}+10\hat{j}-9\hat{k})$  and $C(-5\hat{i}-6\hat{k})$  is 

Answer:

Explanation:

Equation of plane passing through any three  given point is 

$\begin{bmatrix}x-x_{1} &y-y_{1}&z-z_{1} \\x_{2}-x_{1} & y_{2}-y_{1}&z_{2}-z_{1}\\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1} \end{bmatrix}$

   Points are (-2,6,-6),(-3,10,-9) and (-5,0,-6)

 $\Rightarrow$   $\begin{bmatrix}x+2 &y-6&z+6 \\-1 & 4&-3\\-3&-6&0 \end{bmatrix}=0$

$\Rightarrow$  $(x+2)(0-18)-(y-6)(0-9)+(z+6)(6+12)$=0

$\Rightarrow$    $-18(x+2)+9(y-6)+18(z+6)=0$

$\Rightarrow$     $-18x+9y+18z=36+54-108$

$\Rightarrow$    $-2 \hat{i}+\hat{j}+2\hat{k}=-2$

$\Rightarrow$   $2\hat{i}-\hat{j}-2\hat{k}=2$

$\therefore$    $r.(2\hat{i}-\hat{j}-2\hat{k})=2$

In a $\triangle$ ABC, sin A and sin B satisfy   $c^{2}x^{2}-c(a+b)x+ab=0$ , then 

Answer:

Explanation:

 We have,

  $c^{2}x^{2}-c(a+b)x+ab=0$

$\Rightarrow$   $c^{2}x^{2}-cax-cbx+ab=0$

$\Rightarrow$   $cx(cx-a)-b(cx-a)=0$

$\Rightarrow$  (cx-a)(cx-b)=0

$\Rightarrow$   cx-a=0 or cx-b=0

 $\Rightarrow$        $x=\frac{a}{c}$ and x=$\frac{b}{c}$

 As, sin A and sin B  are roots of the given equation 

Let $\sin A= \frac{a}{c}$  and $\sin B =\frac{b}{c}$

$\Rightarrow$        $c= \frac{a}{\sin A}$  and c=$\frac{b}{\sin B}$

$\Rightarrow$    $\frac{a}{\sin A}=\frac{b}{\sin B}=c$  ...........(i)

Using sine law, $\frac{a}{\sin A}$=$\frac{b}{\sin B}$=$\frac{c}{\sin C}$   .............(ii)

So, $\frac{c}{\sin c}=c$[From eqs.(i) and (ii) ]

$\Rightarrow$     $\sin c= \frac{c}{c}$

$\Rightarrow$    $\ sin C=1$       [$\because  \sin \frac{\pi}{2}=1$]

$\Rightarrow$    $\angle C=\frac{\pi}{2}$

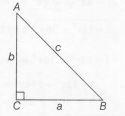
    $\sin A= \frac{a}{c}$ and $\cos A= \frac{b}{c}$

$\therefore$       $\sin A+\cos A= \frac{a}{c}+\frac{b}{c}= \frac{a+b}{c}$

If $\alpha$  is a root of $z^{2}+z+1=0$  , then 

$\left(\alpha^{2014}+\frac{1}{\alpha^{2014}}\right)+\left(\alpha^{2015}+\frac{1}{\alpha^{2015}}\right)^{2}$

$+\left(\alpha^{2016}+\frac{1}{\alpha^{2016}}\right)^{3}+\left(\alpha^{2017}+\frac{1}{\alpha^{2017}}\right)^{4}+\left(\alpha^{2018}+\frac{1}{\alpha^{2018}}\right)^{5}$=

Answer:

Explanation:

 $z^{2}-z+1=0$    then $z=-\omega$

So,   $| (-\omega)^{2014}+\frac{1}{(-\omega)^{2014}}|+\left[(-\omega)^{2015}+\frac{1}{(-\omega)^{2015}}\right]^{2}$

$\left[ (-\omega)^{2016}+\frac{1}{(-\omega)^{2016}}\right]^{3}+\left[(-\omega)^{2017}+\frac{1}{(-\omega)^{2017}}\right]^{4}+\left[(-\omega)^{2018}+\frac{1}{(-\omega)^{2018}}\right]^{5}$

$\left[-\omega-\frac{1}{\omega}\right]+\left[\omega^{2}+\frac{1}{\omega^{2}}\right]^{2}+8+\left[-\omega+\frac{1}{-\omega}\right]^{4}+\left[\omega^{2}+\frac{1}{\omega^{2}}\right]^{5}$

  $=[+\omega+\omega^{2}]+[\omega^{2}+\omega]^{2}+8+[-\omega-\omega^{2}]^{4}+[\omega^{2}+\omega]^{5}$

   =-1+1+8+1+1-1=8

• Mathematics - General questions